5.TP2 : Réfraction de la lumière
Compétences mises en jeu
• Connaitre le principe de propagation rectiligne de la lumière.
• Exploiter les lois de Snell-Descartes pour la réflexion et la réfraction.
• Tester les lois de Snell-Descartes à partir d’une série de mesures et déterminer l’indice de réfraction d’un milieu.
Matériel :
Au bureau
- ☐ Papier millimétré
- ☐ Feuilles blanches
Sur les paillasses des élèves
- ☐ 1 parallélépipède de plexiglas
- ☐ 3 réticules
- ☐ 1 rapporteur photocopié sur un transparent
Préambule
Expérience de la pièce magique
🖉 Décrire l'expérience proposée par le professeur
I - Trajet des rayons lors lors d'un changement de matière
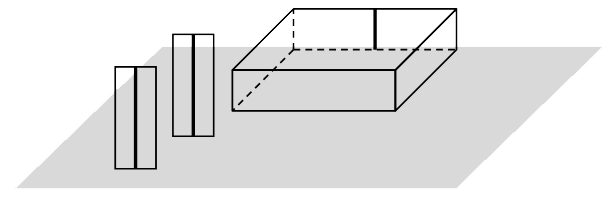
1 - Dispositif expérimental
Le matériel à utiliser est :
- - une feuille,
- - un bloc de plexiglas avec un trait vertical sur l’une des faces (ce trait constitue l’objet à viser),
- - deux réticules (trait vertical sur un support en plastique).
🖑 Tracer sur la feuille le contour du morceau de plexiglas. Représenter également la position du trait par un point noté O.
2 - Tracé des rayons
🖑 Procéder à une première visée du trait à travers le morceau de plexiglas :
- - placer les deux réticules et repérer leurs positions,
- - tracer le trajet du rayon dans l’air en indiquant le sens de propagation de la lumière,
- - compléter le trajet du rayon dans le plexiglas jusqu’au point O.
🖑 Répéter l’opération de façon à obtenir les trajets de 6 à 10 rayons.
3 - Mesures des angles d’incidence et des angles de réfraction
🖑 Pour chaque trajet de la lumière :
- - tracer la normale à l’interface au point d’incidence,
- - mesurer l’angle d’incidence et l’angle de réfraction.
🖉 Compléter le tableau ci-dessous.
| Angle d'incidence i (en °) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Angle de réfraction r (en °) | |||||||||
II - Comparaison avec les théories historiques
1 - Théories
Claude Ptolémée (IIe siècle)
Les rayons perpendiculaires à l’interface ne sont pas déviés.
Johannes Kepler (astronome allemand, 1571 – 1630)
Lorsque les angles d’incidence et de réfaction sont petits, ils sont proportionnels.
Willebrord Snell (astronome et mathématicien hollandais, 1580 -1626) et René Descartes (philosophe et mathématicien français, 1596 – 1650)
Les sinus des angles d’incidence sont proportionnels aux sinus des angles de réfraction.
2 - Confrontation des théories avec l’expérience
a - Théorie de Ptolémé
🖉 Les observations de Ptolémée vous semblent-elle correctes ?
b - Théorie de Kepler
🖉 Calculer le rapport i/r pour les angles d’incidence inférieurs à 20° (compléter la troisième ligne du tableau). L’observation de Kepler vous semble-t-elle correcte ?
c - Théorie de Willebrord Snell et René Descartes
🖉 Proposer une démarche (à partir de vos valeurs d’angles) qui permette de confirmer ou d’infirmer la relation proposée par Snell et Descartes.
